Tutorial R : Cara Menggunakan Linear Regression di Pemrograman R Terbaru

Analisis regresi adalah alat statistik yang sangat banyak digunakan untuk membangun model hubungan antara dua variabel. Salah satu variabel tersebut disebut variabel prediktor yang nilainya dikumpulkan melalui eksperimen. Variabel lainnya disebut variabel respon yang nilainya diturunkan dari variabel prediktor.

Dalam Regresi Linier kedua variabel ini dihubungkan melalui suatu persamaan, di mana eksponen (pangkat) dari kedua variabel tersebut adalah 1. Secara matematis, hubungan linier merepresentasikan garis lurus jika diplot sebagai grafik. Hubungan non-linier di mana eksponen variabel apa pun tidak sama dengan 1 membuat kurva.

Persamaan matematika umum untuk regresi linier adalah -

y = ax + b

Berikut adalah deskripsi parameter yang digunakan -

• y adalah variabel respon.

• x adalah variabel prediktor.

• a dan b adalah konstanta yang disebut koefisien.

Langkah-langkah untuk Menetapkan Regresi

Contoh sederhana dari regresi adalah memprediksi berat badan seseorang saat tinggi badannya diketahui. Untuk melakukan ini kita perlu memiliki hubungan antara tinggi dan berat badan seseorang.

Langkah-langkah untuk menciptakan hubungan tersebut adalah -

• Lakukan eksperimen untuk mengumpulkan sampel nilai tinggi yang diamati dan berat yang sesuai.

• Buat model hubungan menggunakan fungsi lm () di R.

• Temukan koefisien dari model yang dibuat dan buat persamaan matematika menggunakan ini

• Dapatkan ringkasan model hubungan untuk mengetahui kesalahan rata-rata dalam prediksi. Juga disebut residu .

• Untuk memprediksi berat orang baru, gunakan fungsi predict () di R.

Memasukan data

Di bawah ini adalah contoh data yang mewakili pengamatan -

# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131

# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48

lm () Fungsi

Fungsi ini menciptakan model hubungan antara prediktor dan variabel respon.

Sintaksis

Sintaks dasar untuk fungsi lm () dalam regresi linier adalah -

lm(formula,data)

Berikut adalah deskripsi parameter yang digunakan -

• rumus adalah simbol yang mempresentasikan hubungan antara x dan y.

• data adalah vektor di mana rumus akan diterapkan.

Buat Model Hubungan & dapatkan Koefisien

Demo Langsung

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(relation)

Ketika kita menjalankan kode di atas, hasilnya adalah sebagai berikut -

Call:
lm(formula = y ~ x)

Coefficients:
(Intercept)            x  
   -38.4551          0.6746 

Dapatkan Ringkasan Hubungan tersebut

Demo Langsung

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(summary(relation))

Ketika kita menjalankan kode di atas, hasilnya adalah sebagai berikut -

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q     Median      3Q     Max 
-6.3002    -1.6629  0.0412    1.8944  3.9775 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -38.45509    8.04901  -4.778  0.00139 ** 
x             0.67461    0.05191  12.997 1.16e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared:  0.9548,    Adjusted R-squared:  0.9491 
F-statistic: 168.9 on 1 and 8 DF,  p-value: 1.164e-06

fungsi predict ()

Sintaksis

Sintaks dasar untuk predict () dalam regresi linier adalah -

predict(object, newdata)

Berikut adalah deskripsi parameter yang digunakan -

• objek adalah rumus yang sudah dibuat menggunakan fungsi lm ().

• newdata adalah vektor yang berisi nilai baru untuk variabel prediktor.

Memprediksi berat orang baru

Demo Langsung

# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)

# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <-  predict(relation,a)
print(result)

Ketika kita menjalankan kode di atas, hasilnya adalah sebagai berikut -

       1 
76.22869 

Visualisasikan Regresi Secara Grafis

Demo Langsung

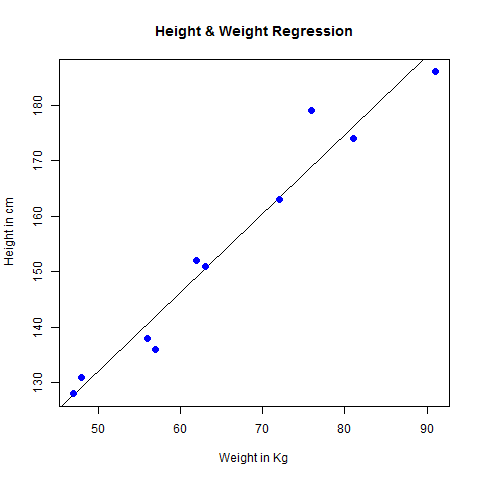
# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)

# Give the chart file a name.
png(file = "linearregression.png")

# Plot the chart.
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")

# Save the file.
dev.off()

Ketika kita menjalankan kode di atas, hasilnya adalah sebagai berikut -

Share :